Statistik selalu digunakan ketika parameter yang menggambarkan karakteristik populasi tidak diketahui. Statistik akan mengambil sebagian (kecil) dari populasi untuk dilakukan pengukuran, kemudian hasil pengukuran tersebut dijadikan sebagai kesimpulan terhadap keseluruhan populasi. Sebagian (kecil) dari populasi tersebut dinamakan sampel. Ibarat kita ingin mengetahui rasa sepanci sayur asam, kita tidak perlu menenggak satu panci tapi cukup mencicipinya sebanyak satu sendok.
Terdapat dua jenis statistik yang digunakan ketika penelitian, yaitu: statistik deskriptif (descriptive statistics) dan statistik inferensi (inferential statistics). Statistik deskriptif hanya menggambarkan data atau seperti apa data ditunjukkan, sementara statistik inferensi mencoba untuk mencapai kesimpulan (bersifat induktif) dari data dengan kondisi yang lebih umum (Trochim, 2006), misal: point estimation, confidence interval estimation, hypothesis testing.
Statistik deskriptif adalah metode-metode yang berkaitan dengan pengumpulan dan penyajian suatu gugus data sehingga menaksir kualitas data berupa jenis variabel, ringkasan statistik (mean, median, modus, standar deviasi, etc), distribusi, dan representasi bergambar (grafik), tanpa rumus probabilistik apapun (Walpole, 1993; Correa-Prisant, 2000; Dodge, 2006). Pada SPSS, analisis statistik deskriptif dilakukan dengan meng-klik menu Klik [Analyze] -> [Descriptive Statistics], kemudian terdapat pilihan: Frequencies, Descriptives, Explore, Crosstabs, dan Ratio. Dalam penelitian-penelitian, perintah-perintah ini sering diabaikan karena memang dalam beberapa fungsi analisis lain sudah otomatis tercantum analisis deskriptifnya.
Dengan data sebagaimana ditunjukkan Tabel 1 di bawah ini, kita akan mempraktekkan operasi submenu Frequencies, Descriptives, Explore, dan Crosstabs. Fungsi Ratio tidak akan dibahas karena bagi saya; yang belajar di SPSS 11, ini tergolong baru

, fasilitas Ratio mulai diperkenalkan pada SPSS versi 11.5, pada dasarnya berfungsi menyediakan ringkasan statistik yang berupa rasio-rasio.
Tabel 1
Data Nilai Mahasiswa (bukan data sebenarnya)
Nama Usia Jenis Kelamin Nilai APK Nilai PPC Nilai PLO
Suhairi 20 Laki-Laki 80 50 70
Ambon 21 Laki-Laki 70 70 90
Astri 22 Perempuan 60 80 70
Henri 21 Laki-Laki 80 90 60
Yugos 22 Laki-Laki 90 60 70
Muji 19 Perempuan 70 80 80
Tatang 20 Laki-Laki 60 70 40
Ferdi 21 Laki-Laki 60 90 60
Arsyad 21 Laki-Laki 70 70 40
Fauzan 21 Laki-Laki 90 80 60
*) Laki-Laki (Value: 1), Perempuan (Value: 2)
Langkah pertama yang perlu dilakukan adalah meng-entry data, tentunya anda perlu paham dasar-dasar SPSS (silahkan baca posting sebelumnya yang berjudul:
Dasar-Dasar SPSS). Entry data dilakukan pada tab sheet Data View setiap baris mewakili satu responden, sedangkan setiap kolom mewakili satu variabel, dalam kasus ini variabelnya adalah: Nama, Usia, Jenis Kelamin, Nilai APK, Nilai PPC, dan Nilai PLO. Berikut langkah-langkah entry datanya:
Masukkan variabel: Nama untuk “Nama”, Usia untuk “Usia”, Gender untuk “Jenis Kelamin”, APK untuk “Nilai APK”, PPC untuk “Nilai PPC”, dan PLO untuk “Nilai PLO” pada kolom Name pada tab sheet [Variable View].
Berilah label untuk masing-masing variabel dengan menuliskannya pada kolom Label: Usia, Jenis Kelamin, Nilai APK, Nilai PPC, dan Nilai PLO. Hal ini berarti: variabel Gender mempunyai label “Jenis Kelamin”, variabel APK mempunyai label “Nilai APK”, dan seterusnya.
Untuk variabel Gender pada kolom Values, definisikan Value: 1 = Laki-laki dan Value: 2 = Perempuan.
Untuk variabel Nama (baris pertama ) pada kolom Type, ubah tipe data menjadi String.
Pada kolom Decimals isi nol untuk semua variabel.
Untuk kolom lainnya seperti Width, Missing, dan Columns biarkan tetap default SPSS.
Jangan lupa ”save” atau tekan Ctrl + S. Secara default SPSS akan memberi nama file: data_1.sav, saya merubah nama file menjadi eRiskProject_1.sav.
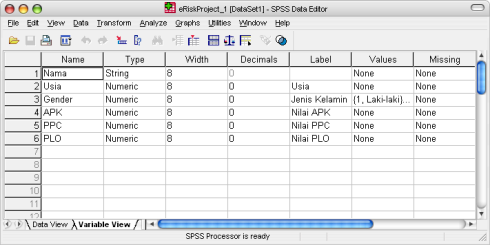
Gambar 1. Entry Variabel pada Tab Sheet Variable View
Kemudian klik tab sheet [Data View] dan mulailah meng-entry data seperti yang diperlihatkan Gambar 2 di bawah ini.
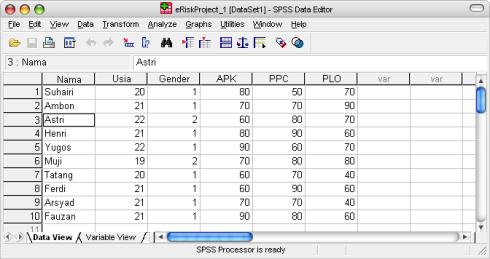
Gambar 2. Entry Data pada Tab Sheet Data View
Untuk melihat hasil definisi Value pada variabel Gender, klik ikon

, variabel Gender akan terdefinisi menjadi laki-laki dan perempuan, tidak lagi berisi angka 1 dan 2.
Selanjutnya, kita ingin menjumlahkan nilai APK, PPC, dan PLO, Klik menu [Transform] –> [Compute], muncul dialog box Compute Variable.
Buatlah variabel baru dengan nama “total” untuk menempatkan hasil penjumlahan nilai APK, PPC, dan PLO, caranya: tuliskan “total” pada form Target Variable. Kemudian Klik [Type & Label], beri label “Nilai Total“.
Ketik “APK + PPC + PLO” (sesuai nama variabel dan perintah penjumlahan ) pada form Numeric Expression. Anda juga dapat menggunakan tombol-tombol yang tersedia pada dialog box, lihat Gambar 3.

Gambar 3. Contoh Perintah Penjumlahan pada Dialog Box Compute Variable
Klik [OK]. Pada Data View akan muncul variabel baru dengan nama “Total” (lihat Gambar 4).
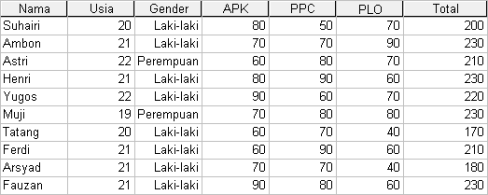
Gambar 4. Output dari Perintah Penjumlahan pada Dialog Box Compute Variable
Setelah data di-entry, selanjutnya memulai menggunakan perintah-perintah statistik deskriptif. Tahap pertama adalah menggunakan perintah Frequencies.
1. Frequencies
Perintah Frequencies digunakan untuk memperoleh jumlah pada nilai-nilai sebuah variabel tunggal. Langkah-langkahnya adalah sebagai berikut:
Klik menu [Analyze] -> [Descriptive Statistics] -> [Frequencies].
Muncul dialog box Frequencies. Klik “Jenis Kelamin [Gender]” ‐> klik

, (untuk memasukkan variabel Jenis Kelamin ke form Variables(s). Kita akan menganalisis variabel Jenis Kelamin.
Jangan lupa centang Display frequency tables.
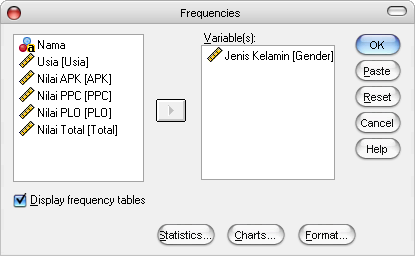
Gambar 5. Dialog Box Frequencies
Agar menampilkan representasi bergambar (grafik), klik [Charts], maka akan muncul dialog box Frequencies: Charts. Saya memilih Bar charts pada form Chart Type. Pada form Chart Values , saya memilih Percentages (Lihat Gambar 6).
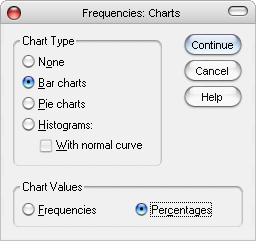
Gambar 6. Menampilkan Bar Charts pada Dialog Box Frequencies: Charts
Kemudian klik [Continues] untuk kembali ke dialog box Frequencies lalu klik [OK] maka muncul jendela SPSS Viewer yang menunjukkan hasil analisis frekuensi (lihat Gambar 7).
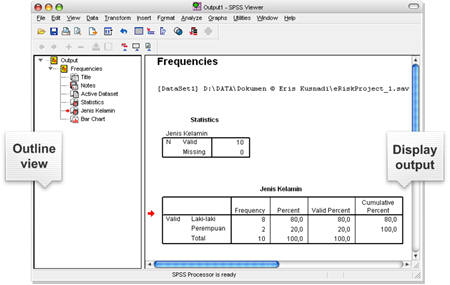
a) Sebelah kiri adalah Outline view dalam bentuk tree files, fungsinya sebagai navigasi dalam melihat outputanalisis.
b) Sebelah kanan adalah Display output, fungsinya menampilkan seluruh hasil analisis yang telah kita lakukan.
Gambar 7. Display Output pada SPSS Viewer
Pada Gambar 7 terlihat hasil analisis SPSS, di mana pada tabel pertama N Valid = 10 yang menunjukkan jumlah responden 10 orang dan N Missing = 0 yang berarti tidak ada data yang hilang (missing). Pada tabel yang kedua terlihat hasil analisis Frequencies terhadap variabel Jenis Kelamin, di mana jumlah responden laki-laki 8 orang (80%) dan responden perempuan ada 2 orang (20%). Jika scroll digeser ke bawah akan terlihat Bar Chart (lihat Gambar 8) yang menunjukkan visualisasi jumlah responden laki-laki dan perempuan.

Gambar 8. Bar Chart
Perhatikan kriteria “laki-laki” dan “perempuan“, ini merupakan hasil definisi value variabel Gender pada kolom Values, di mana Value: 1 = Laki-laki dan Value: 2 = Perempuan. Jika definisi value diabaikan maka pada bar chart maupun tabel analisis yang terlihat bukan laki-laki dan perempuan melainkan 1 dan 2. Begitu juga judul tabel dan judul histogram: “jenis kelamin“, ini merupakan hasil dari proses label yang telah kita lakukan untuk variabel Gender. Fungsi label ini bermanfaat untuk para pembaca analisis, misal penguji pada sidang Tugas Akhir / Skripsi. Selanjutnya adalah penggunaan perintah Descriptives.
2. Descriptives
Dengan menggunakan data sebelumnya langkah-langkah perintah Descriptives adalah sebagai berikut:
Klik menu [Analyze] -> [Descriptives Statistics] -> [Descriptives].
Muncul dialog box Descriptives. Masukkan variabel yang akan dianalisis ke form Variables(s). Untuk melakukan setting optional klik [Options].
Muncul dialog box Descriptives: Options. Centang analisis yang diperlukan. Dalam hal ini pilihannya adalah: Mean, Std. deviation, Minimum, Maximum, Kurtosis, Skewness, dan pada form Display Order centang Variable list.
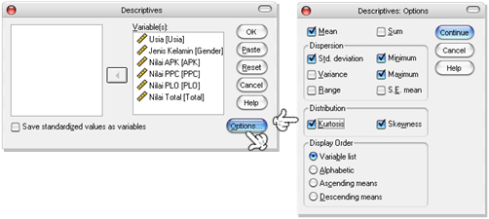
Gambar 9. Langkah-Langkah Descriptives Statistics
Klik [Continue] dan [OK]. Hasil analisis akan terlihat seperti tabel yang ditunjukkan Gambar 10 di bawah ini:

Gambar 10. Output Descriptives
Tabel output di atas menunjukkan jumlah pengukuran (N), nilai minimum (Minimum), nilai maksimum (Maximum), nilai rata-rata (Mean), standar deviasi (Std.), Skewness, dan Kurtosis dari masing-masing variabel. Nilai skewness merupakan ukuran kesimetrisan histogram, sedangkan kurtosis merupakan ukuran datar atau runcingnya histogram. Idealnya nilai skewness dan kurtosis pada distribusi normal adalah nol. Oleh karena itu:
Jika nilai skewness positif maka distribusi data “miring ke kiri distribusi normal” (ada frekuensi nilai yang tinggi di sebelah kiri titik tengah distribusi normal), sebaliknya apabila skewness negatif maka distribusi data ”miring ke kanan distribusi normal” (kiri bagi kita yang melihatnya).
Jika nilai kurtosis positif maka distribusi data “meruncing” (ada satu nilai yang mendominasi), sebaliknya apabila Kurtosis Negatif maka distribusi data “melandai” (varians besar).
Perhatikan Gambar 10 di atas, variabel Usia memiliki skewness negatif dan kurtosis positif, artinya distribusinya “miring ke kiri distribusi normal” dan “meruncing”. Pada variabel nilai APK, nilai skewness positif dan nilai kurtosis negatif, artinya distribusinya “miring ke kanan distribusi normal” dan “melandai”. Sebagai pembuktian, buat histogram untuk variabel Usia dan Nilai APK. Berikut caranya:
Klik menu [Graphs] -> [Histogram], maka muncul dialog boxHistogram.
Pilih variabel Usia dan masukkan dalam form Variable.
Centang Display normal curve, untuk memperlihatkan kurva normal.
Selanjutnya klik [OK].
Lakukan langkah yang sama untuk variabel nilai APK. Hasilnya bisa dilihat pada Gambar 12.
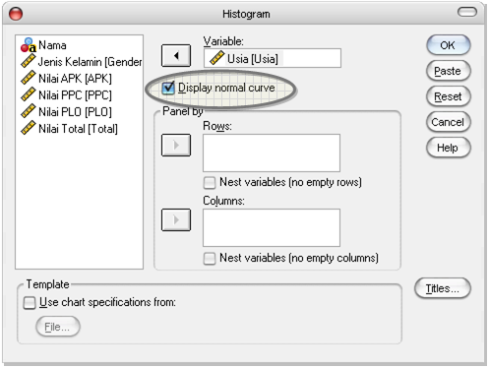
Gambar 11. Menampilkan Histogram bersama Kurva Normal

Gambar 12. Analisis Skewness dan Kurtosis pada Histogram
Gambar 12 di atas menunjukkan histogram untuk variabel Usia memiliki distribusi “miring ke kiri distribusi normal” karena nilainya skewness negatif dan “meruncing” karena nilai kurtosis positif. Sebaliknya, histogram untuk variabel Nilai APK memiliki distribusi “miring ke kanan distribusi normal” karena nilainya skewness positif dan “melandai” karena nilai kurtosis negatif. Di sini, anda bisa menentukan apakah distribusi tersebut normal atau tidak. Anda bisa saja menyatakan normal, karena menyerupai bentuk lonceng tetapi agak serong, tapi orang lain mungkin akan menyatakan tidak normal karena jauh dari bentuk lonceng. Jika sulit mengambil keputusan, silahkan lakukan pengujian normalitas yang lebih advance, misal dengan Uji Kolmogorov-Smirnov. Selanjutnya, kita masuk pada penggunaan perintah Explore.
3. Explore
Perintah Explore digunakan untuk membandingkan antara dua atau lebih kelompok dengan satu variabel. Sebagai contoh, jika kita menggunakan Jenis Kelamin sebagai variabel independen; variabel ini mendefinisikan kelompok (Laki-Laki dan Perempuan), kemudian membandingkannya dengan variabel lain, seperti Usia. Perintah Explore; contoh dalam kasus mean, akan menghasilkan berapa rata-rata usia laki-laki dan berapa rata-rata usia perempuan. Ukuran-ukuran yang dihasilkan perintah Explore antara lain: ukuran-ukuran pemusatan data (mean dan median), ukuran penyebaran (range, interquartile range, standar deviasi, varians, minimum, dan maksimum), ukuran kurtosis, dan skewness.
Berikut langkah-langkah perintah Explore:
Klik menu [Analyze] -> [Descriptives Statistics] -> [Explore].
Muncul dialog box Explore.
form Factor List, isi: variabel Jenis Kelamin.
form Dependent List, isi: variabel Usia, Nilai APK, Nilai PPC, Nilai PLO, dan Nilai Total.
Form Display ada tiga pilihan Both, Statistics, dan Plots. Saya hanya memilih [Statistics].
Klik [Plots] bila perlu grafik boxplot.
Klik [Statistics] bila tidak perlu grafik boxplot.
Klik [Both] bila perlu keduanya.
Terakhir klik [OK].

Gambar 13. Dialog Box Explore

Gambar 14. Contoh Output Explore untuk Variabel Usia
Selanjutnya, kita masuk pada penggunaan perintah Crosstabs.
4. Crosstabs
Jika perintah Frequencies digunakan untuk memperoleh jumlah pada nilai-nilai sebuah variabel tunggal, perintah Crosstabs digunakan untuk memperoleh jumlah pada nilai-nilai lebih dari satu variabel. Apabila analisis statistik deskriptif sebelumnya mengolah data secara keseluruhan dalam setiap variabel dengan menghitung perhitungan statistik seperti Mean, Standar deviasi, Kurtosis, etc. Pada Crosstabs, setiap nilai pada variabel yang dianalisis dijabarkan jumlahnya, dengan begitu kita dapat mengetahui berapa jumlah subyek laki-laki yang berusia 19 tahun, 20 tahun, dst. Deskripsi data pada Crosstabs akan disajikan dalam bentuk tabel silang (crosstab) yang terdiri dari baris dan kolom.
Berikut langkah-langkah perintah Crosstabs:
Klik menu [Analyze] -> [Descriptives Statistics] -> [Crosstabs].
Muncul dialog box Crosstabs.
form Column(s), isi: variabel Jenis Kelamin.
form Row(s), isi dengan variabel yang akan dianalisis, dalam hal ini isi dengan variabel Usia.

Gambar 15. Dialog Box Crosstabs
Klik pilihan [Display clustered bar charts], pilihan ini untuk menampilkan chart bar dari output.
Untuk dialog box [Statistics], [Cells], dan [Format] biarkan sesuai dengan default SPSS.
Terakhir klik [OK].

Gambar 16. Output Crosstabs
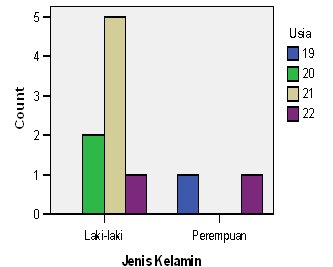
Gambar 17. Clustered Bar Charts
Statistik deskriptif memberikan informasi inti dari kumpulan data, seperti ukuran-ukuran pemusatan data (mean dan median), ukuran penyebaran (range, interquartile range, standar deviasi, varians, minimum, dan maksimum), ukuran kurtosis, dan skewness serta representasi piktorialnya. Tabel, diagram, dan grafik yang sering ditemukan di majalah dan koran-koran merupakan salah satu contoh penggunaan statistik deskriptif.

































